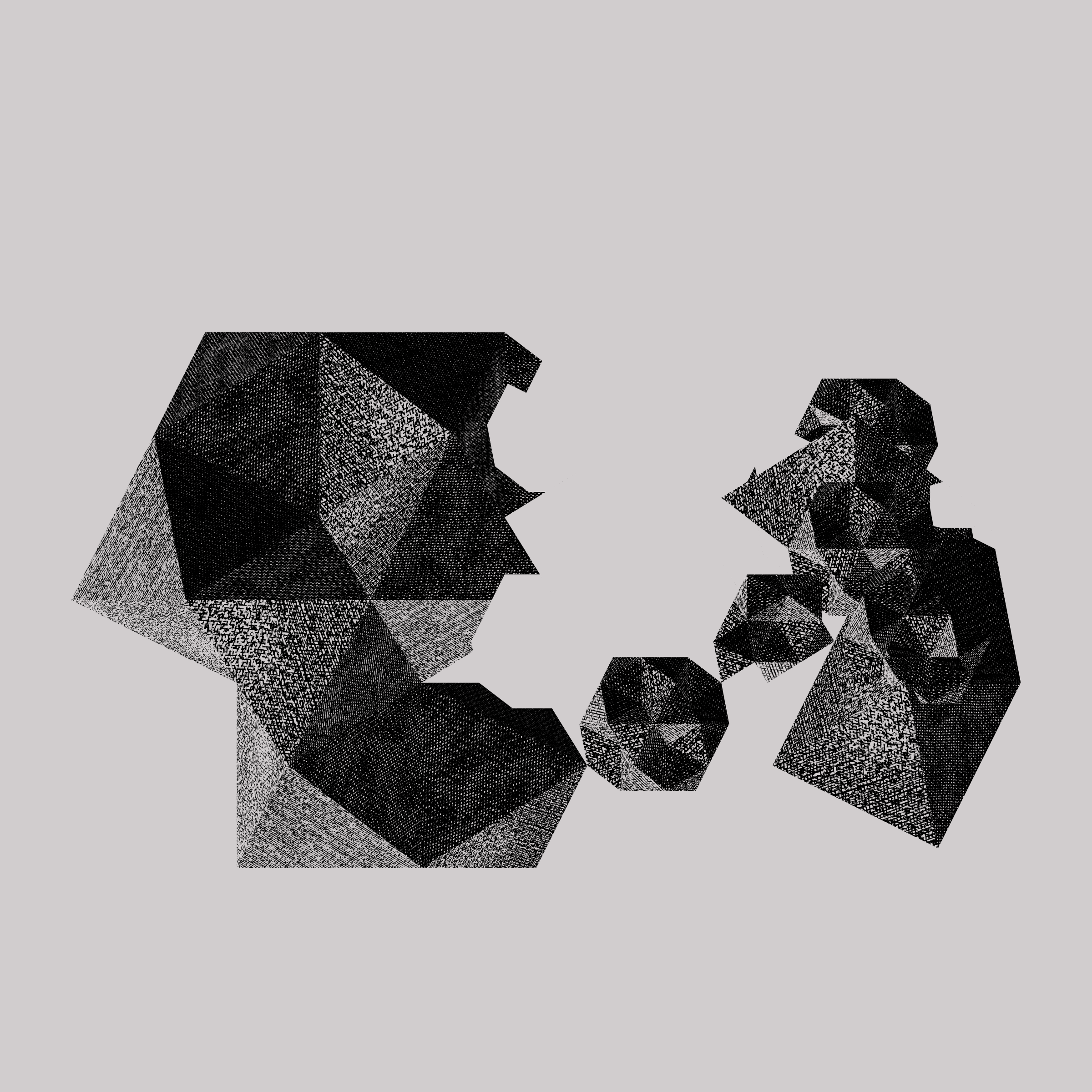This site uses cookies – More Information.
Primitives
Two sources from the worlds of science and art inspired the project: Albrecht Dürer’s Engravings and the phenomena of Quasicrystals. Together, they create a project about drawing infinity through a novel geometric block.

DURER'S ENGRAVINGS
Albrecht Dürer and his masterpiece Melencholia I (1514) inspired us to dive deep into the process of engraving reinterpreted through the medium of code. Eight Durer hatches were developed for Primitives. Durer not only perfected a new medium but invented an early imaging technology. By scratching metal away from a plate, an inversion of conventional drawing, engraving allowed a work of art to be reproduced and disseminated widely. For the blockchain, a new kind of dissemination, we developed a Durer 3-bit shader (2^3 = 8 values); the anachronism of the engravers trade translated into pure 1’s and 0’s.

QUASICRYSTALS
Primitives is based on the science of quasicrystals. Unlike a regular crystal, whose molecular pattern is periodic (or repetitive in all directions), the distinctive quality of a quasicrystal is that its structural pattern never repeats the same way twice. It is ordered but aperiodic. Endless and uneven, quasicrystals can be described by the precise arrangement of a single modular part. As these small units aggregate together they form larger figures that themselves combine into ever larger movements, always a little bit different from any other. In this sense, quasicrystalline patterns have an infinite capacity to create and carry information.
Controls
‘arrow keys’ rotate view
‘i’ saves image
FEATURE SET
The feature set probes the unique properties of the Primitives crystalline growth, their fractal depth and lattices. We also looked closely at the process of engraving to inform the variability in representation, from different inked backgrounds to paper colors. There are even incomplete and fragmented drawings which were inspired from Durer’s sketches. Overall the feature set is rigorously designed to balance variety and uniqueness with conceptual aims.

400 Primitives minted outputs in PixPlot, a convolutional neural network and Uniform Manifold Approximation and Projection (UMAP) in order to cluster visually similar images near one another.
OUTPUTS
Primitives is an exploration of endlessness. The infinite is immanent in every block or, in terms of contemporary scientific thinking, the entire universe is contained within every piece of it. Here are some ways we’ve imagined outputting Primitives in the physical world.
CLUSTER ANALYSIS
These clusters are an intuitive, highly subjective response to the mint outputs. They are clustered by unexpected character, not necessarily rarity, although sometimes that’s part of it.

THE DARK SIDE
This cluster is unexpectedly dark, with the foreground Primitives in shadow against the rare dark hatch background. There is something brooding about these moonlit arrangements.

THE INCOMPLETES
These are inspired by Durer’s engraving process where part of the work is still blank. They don’t happen very often and if you spin them around you’ll see that the missing primitives are still there, sort of, but incomplete in 3D.

SKETCH MODE
These are also incomplete “proofs” that show sketch lines before the engraving is hatched. Primitives appear like wireframes. Because they are rare, we were surprised that the first two mints were sketches.

The ZOOMS
A special thing about these zoomed-in token images is that while they capture a specific Primitives up close and personal, they also reveal intimate details of all the Primitives.

SPEED DEMONS
This cluster is fast, the linear backgrounds create a strong sense of movement. While we started with Durer engravings, we somehow ended up on classic Manga.

DEEP FRACTALS
These outputs share the feature of “Deep” fractal depth meaning they have the maximum allowable (three) fractal generations of primitives in large quantities. A mouthful but it basically means these Primitives are complex.

FIGURES
The six types of growth produce recognizable figures.
Read our essay Ragged Edges about the history of the quasicrystal to learn more.



Sharing some of the Primitives code.
document.oncontextmenu = () => false;
var cam;
//Grow class
let grw;
//lists to hold information in a "stack"
let go = [];
let gScale = 20; //starting octahedra scale
let gSize; //global for holding the size of a GO, for rem dups
//Current items
let currGo; //the current Golden Octahedra
let currFace; //the current Face to grow from
let currPoint;//the current point we are "starring" around
let currColor; //the current color
let baseColor;
//drawing vars
let steps = 0;
let stepSize = 1;
let stepStart = 0;
//target point
let targetPt; //point to grow to, on update (vector)
let randAlpha = 0.8; //likely hood of scaling from any unit during "grow" "decorate"
let currArraySize = 0; //keep track of the number of units every grow cycle
//Grid vars
let rg; //Grid Object
let gLayers = 5;
let gWidth = 5;
let gHeight = 5;
let currGPt = 0;
//fade variables
let delayCnt = 0;
let delayNum = 0;
let numPts = 6; //The number of pts in the bridge
let ptCnt = 0; //
//Lighting
let sun = new p5.Vector(0,1,1);
sun.normalize();
let img = [];
function preload() {
// Load the textures
for(let i=0; i<7; i++){
img[i] = loadImage('data/0' + (i+1) + '.jpg');
}
}
function setup() {
createCanvas(800, 800, WEBGL);
//frameRate(30);
// define initial state
var state = {
distance :
300,
rotation :
Dw.Rotation.create( {
angles_xyz:
[0, 0, 0]
}
),
};
cam = new Dw.EasyCam(this._renderer, state);
//set up grow system target pts
grw = new GrowSys(1);
//console.log("my gens = " + grw.gens);
//Create the Grid
rg = new Grid_Rhomb(gWidth, gHeight, gLayers,gScale);
//initial target point, center of grid
targetPt = rg.gPts[0][floor(gWidth/2)][floor(gHeight/2)];
//targetPt = rg.gPts[0][2][2];
//Seed, create GO by Verts
go.push(new Go3d(1,targetPt.x, targetPt.y, targetPt.z, gScale, baseColor));
currGo = go[0];
//go.push(new Go3d(2,undefined,undefined,undefined,undefined,undefined,currGo.faces[1],currGo.verts));
}
function draw() {
background (17,17,17);
// projection
var cam_dist = cam.getDistance();
var oscale = cam_dist * 0.001;
var ox = width / 2 * oscale;
var oy = height / 2 * oscale;
ortho(-ox, +ox, -oy, +oy, -10000, 10000);
cam.setPanScale(0.004 / sqrt(cam_dist));
let locX = mouseX - width / 2;
let locY = mouseY - height / 2;
//pointLight(219,188,102, 800,0,800) // Adds a directional light (color object)
//spotLight(222, 222, 222, locX, locY, 800, 0, 0, -3, Math.PI);
//directionalLight(0,0,255, 0,-1,1) // Adds a directional light (color object).
//directionalLight(200,200,200, 0,0,-1)
//pointLight(250, 250, 250, locX, locY, 50)
lightFalloff(0.003, 0.0003, 0);
pointLight(200,200,200, 0,800,0)
ambientLight(78,78,78);
//fade in
if (steps < go.length) {
delayCnt += 1;
if (delayCnt == delayNum+1) {
steps += stepSize; //how many additional objects to draw each frame refresh
delayCnt = 0;
}
}
else if (steps == go.length) { //We're done
delayCnt += 1;
delayCnt = delayNum;
//grw.decorate();
}
//Draw each go
for (let i=stepStart; i<steps; i++) {
go[i].drawGo();
}
/*
//Draw Grid
for (let i=0; i<gLayers; i++) {
for (let j=0; j<gWidth; j++) {
for (let k=0; k<gHeight; k++) {
push();
translate(rg.gPts[i][j][k].x,rg.gPts[i][j][k].y,rg.gPts[i][j][k].z);
fill(180,180,180);
noStroke();
box(3);
pop();
}
}
}
*/
} //end draw
function keyPressed() {
if ((key =='n') || (key == 'N')) {
nextGrow();
}
}
function nextGrow() {
console.log("NEXT GROW");
//Reset
currGPt = 0;
steps = 0;
go = []; //clear the go array
//reseed
go.push(new Go3d(1,targetPt.x, targetPt.y, targetPt.z, gScale));
currGo = go[0];
ptCnt = 0;
//Pick a number of random points to grow through
let rand = 1; //getRandomInt(2)+1;
let bridgePts = [];
for (let i=0; i<rand; i++) {
let rl = gLayers-1; //getRandomInt(gLayers);
let rw = getRandomInt(gWidth);
let rh = getRandomInt(gHeight);
bridgePts[i] = rg.gPts[rl][rw][rh]; //need to weed out dups
}
delayCnt = 0;
//record current array size
currArraySize = go.length;
//grow to new point
for (let i=0; i<bridgePts.length; i++) {
grw.growToTarget(bridgePts[i]);
}
}
function getRandomInt(max) {
return Math.floor(Math.random() * max);
}